Percobaan MENGUKUR KONSTANTA PLANCK

Pendahuluan

Sebelum abad ke-20 cahaya hanya dianggap sebagai gelombang. Semua sifat gelombang dipenuhi oleh cahaya seperti pemantulan, pembiasan, interferensi, dan difraksi. Namun, memasuki abad-20 banyak pengamatan fenomena cahaya yang tidak dapat dijelaskan dengan teori gelombang. Salah satu yang terkenal adalah radiasi benda hitam.

Jika cahaya hanya dianggap sebagai gelombang maka kerapatan energi yang diradiasi benda hitam makin besar jika panjang gelombang makin kecil. Jika panjang gelombang menuju nol maka kerapatan energi yang diradiasi menuju tak berhingga. Teori radiasi benda hitam atas asumsi cahaya merupakan gelombang penuh dikembangkan oleh Rayleigh dan Jeans. Namun, pengukuran yang sangat teliti oleh para fisikawan di akhir abad-19 menunjukkan bahwa jika panjang gelombang cahaya sudah sangat kecil maka kerapatan energi yang dipancarkan makin kecil. Dan ketika panjang gelombang cahaya menuju nol maka kerapatan energi yang dipancarkan menuju nol.

Dengan demikian, kerapatan energi yang dipancarkan benda hitam mula-mula naik dengan mengecilnya panjang gelombang dan mencapai puncak pada panjang gelombang tertentu. Setelah itu, ketika panjang gelombang diperkecil lagi, kerapatan energi radiasi berbalik mengecil hingga menuju nol. Gambar 1 memperlihatkan kurva radiasi benda hitam menurut teori gelombang Rayleigh-Jeans, yang ditandai dengan garis titik-titik. Kurva tebal adalah hasil pengukuran. Tampak bahwa teori Rayleigh-Jenas mendekati hasil pengukuran untuk panjang gelombang sangat besar. Namun menyimpang jauh untuk panjang gelombang kecil. Pada daerah ultraviolet (panjang gelombang sangat kecil), terjadi penyimpangan yang luar biasa. Ramalan teori Rayleigh-Jeans jauh lebih besar daripada hasil pengkuran. Penyimpangan ini sering disebut bencana ultraviolet (ultraviolet catastrophe). Jadi, yang disebut bencana ultraviolet bukan bencana dalam arti sebenarnya. Tetapi penyimpangan teori Rayleigh-Jeasn dengan hasil pengukuran pada daerah ultraviolet.

Karena kegagalan tersebut, Planck merevisi teori radiasi benda hitam. Planck mengusulkan bahwa radiasi benda hitam menyimpan energi dengan nilai yang diskrit yang disebut kuanta. Energi radiasi benda hitam hanya bisa merupakan kelipatan bulat dari nilai tertentu, yang sering disebut kuantisasi energi. Menurut Planck, energi radiasi benda hitam memenuhi

dengan

n adalah bilangan bulat

f adalah frekuensi radiasi benda hitam

h adalah konstanta yang dinamaakn konstanta Planck.

Nilai konstanta Planck sangat kecil, yaitu 6,625 x 10^-34 J s.

Selanjutnya, untuk menjelaskan fenomena fotolistrik, Einsterin berhipotesis bahwa energy cahaya pun terkuantisasi dalam paket-paket. Energi paket cahaya memenuhi e = hf, persis sama dengan energy kuanta dalam radiasi benda hitam. Aakhirnya, para ahli sepakat bahwa energi semua gelombang elektromagnetik terkuantisasi menurut persamaan Einstein.

Pertanyaan menarik bagi kita adalah, dapatkan kita mengukur nilai konstanta Planck yang sangat kecil itu? Di sini akan kita bahas. Memang teori dasar yang digunakan cukup rumit, tetapi hasil akhir cukup sederhana.

Kita mulai dari intensitas radiasi benda hitam yang memiliki suhu T dan pada frekuensi f memenuhi persamaan Planck

dengan

c adalah laju cahaya dalam vakum

k adalah konstanta Boltzmann = 1,38 x 10^-23 J/K

T adalah suhu permukaan benda hitam dalam kelvin

Persamaan (2) menyatakn intensitas pada frekuensi f saja. Namun, intensitas total pada semua frekuensi memenuhi persamaan Stefan-Boltzmann

dengan

sigma adalah konstanta Bolztamann = 5,670373 x 10^-8 W m^-2 K^-4

Jika luas permukaan benda hitam adalah A dan daya yang dipancarkan benda hitam adalah P maka

Dengan demikian, suhu permukaan benda hitam memenuhi persamaan

Suhu kebanyakan benda hitam yang akan digunakan dalam percobaan kurang dari 10.000 K. Pada suhu tersebut nilai perkalian kT masih lebih kecil daripada nilai hf untuk cahaya tampak. Dengan demikian hf/kT >>1 sehinga kita dapat melakukan aproksimasi

dan persamaan (2) dapat diaproksimasi sebagai

atau

Misalkan benda hitam memancarkan daya P₁, maka suhu yang permukaannya adalah T₁ dan intensitas yang dipancarkan pada frekuensi f adalah I₁(f). Dengan demikian, persamaan (6) menjadi

Misalkan benda hitam memancarkan daya P₂, maka suhu yang permukaannya adalah T₂ dan intensitas yang dipancarkan pada frekuensi f adalah I₂(f). Dengan demikian, persamaan (6) menjadi

Bagi persamaan (8) dengan persamaan (7) maka diperoleh

atau

Ambil logaritma natural dua ruas pada persamaan (9) sehingga diperoleh

atau

Persamaan (10) menghasilkan ungkapan untuk konstanta Planck sebagai berikut

Selanjutnya, dengan menggunakan persamaan (5) maka

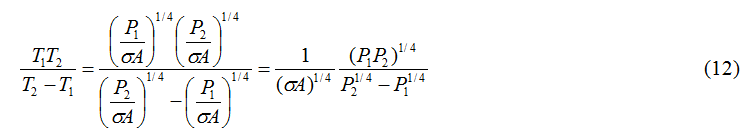
Substitusi persamaan (12) ke dalam persamaan (11) maka diperoleh ungkapan konstanta Plansk sebagai berikut

Yang perlu kita ukur adalah P₁, P₂, f, A, I₁ dan I₂ agar h diketahui. Bagaimana caranya? Kita gunakan susunan alat sebagai berikut.

Perhatikan Gambar 2. Fiamen lampu pijar dianggap sebagai benda hitam. Luas A pada persamaan (13) adalah luas permukaan filamen. Untuk tujuan tersebut maka satu lampu pijar harus dipecahkan agar ukuran permukaan filament dapat ditentukan.

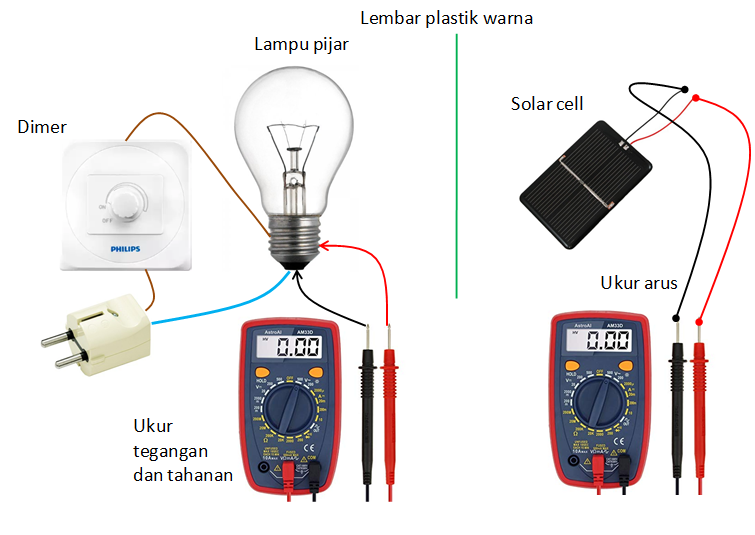
Filamen lampu adalah hambatan yang bisa menahan suku yang sangat tinggi. Hambatan filament dapat dikur dengan voltmeter. Ketika pada dua ujung vilamen terukut tegangan listrik V maka daya kalor yang dihasilkan filemen adalah

dengan

V adalah tegangan antara dua ujung filament

R adalah hambatan filament

Data tersebut berkaitan langsung dengan suhu permukaan filament. Kita dapat menghasilkan dua nilai daya dengn mengatur dimmer. Jadi P₁ dan P₂ dapat kita peroleh. Selanjutnya tinggal menentukan I₁ , I₂ dan f.

Arus yang dihasilkan solar sell sebanding dengan intensitas cahaya yang mengenainya. Jadi

di mana i adalah arus yang dihasilkan solar cell. Dengan demikian

Ini berarti, rasio intensitas cahaay sama dengan rasio arus yang dihasilkan solar cell.

Terakhir adalah menentukan f. Karena kita pasang plastik berwana antara lampu dan solar cell maka kita mengansumsikan bahwa warnha cahaya yang mengenai solar cell sama dengan warna plastik. Dengan menggunakan data di internet, frekuensi yang bersesuaian dengan warta nersebut dapat ditenrukan. Akhirnya semua besaran yang dibutuhkan dapat duiperoleh dan konstanta Planck dapat dihitung.

Tujuan

Mengukur konstanta Plack dengan cara yang sederhana seperti ditunjukkan pada Gambar 2.

Alat/Bahan

1. Lampu pijar
2. Dimmer
3. Kabel
4. Stop contact PLN
5. Saklar
6. Multimeter
7. Plastic transparan berwarna
8. Solar cell
9. Mikorometer

Langkah Perobaan

1. Ukur hambatan filament lampu
2. Buat rangkaian seperti pada Gambar 2
3. Atur dimmer sehingga daya yang dihasilkan maksimum
4. Ukur tegangan antara dua ujung filament
5. Ukur arus yang dihasilkan solar cell
6. Atur dimer sehingga lampu agak redup
7. Ukur tegangan antara dua ujung filamen
8. Ukur arus yang dihasilkan solar cell
9. Ulangi langkah 3-8 dengan menggunakan plastik yang berwarna lain
10. Setelah semua selesai, pecahkan lampu dan ukur (perkirakan) luas pemukaan filament. Pengukuran tersebut mungkin hanya menghasilkan nilai perkiraan. Yang diukur adalah panjang filamen dan ketebalannya (diameter).

Tugas

1. Hitung konstanta Planck berdasarkan data yang diukur.
2. Bandingkan hasil yang diperoleh dengan data di referensi.
3. Jika ada perbedaan, jelaskan kemungkinan penyebab perbedaan tersebut

Jika merasa bermanfaat, silakan share dan like: