222: Fisika SMA: Eksperimen – Pembuktian Persamaan Seri dan Paralel Kapasitor

Kita sudah bahas bahwa jika sejumlah kapasitor dirangkai secara seri maka kapasitansi efektif menjadi lebih kecil. Sebaliknya, jika kapasitor dirangkai secara paralel maka kapasitasi efektif menjadi lebih besar.

Kapasitansi efektif kapasitor yang dirangkai secara seri memenuhi persamaan

\( {1 \over C_t} = {1 \over C_1} + {1 \over C_2} + {1 \over C_3} + … \)

Kapasitansi efektif kapasitor yang dirangkai secara paralel memenuhi persamaan

\( C_t = C_1 + C_2 + C_3 + … \)

Mungkin kita sudah belajar berkali-kali topik ini. Namun semuanya hanya teori. Sangat jarang dilakukan eksperimen langsung untuk membuktikan persamaan tersebut. Sekarang kita akan bahas pembuktian eksperimen.

Apa yang harus kita lakukan? Kita lakukan pengukuran tegangan saat pengisian kapasitor. Kita sudah bahas di bagian 221 bahwa dari kurva pengisian tersebut kita dapat menghitung nilai kapasitansi. Jadi kita ukur kurva pengisian untuk satu kapasitor, dua kapasitor diseri, tiga kapasitor diseri, dua kapasitor diparalel, dan tiga kapasitor di paralel. Dari setiap kurva kita hitung kapasitansi efektif. Dari nilai kapasitansi total kita buktikan bahwa persamaan rangkaian kapasitor dipenuhi.

Bahan yang digunakan

Saya menggunakan tiga buah kapasitor 10 mikrofarad dan tahanan 56 kilo-ohm (warna hijau, biru, dan jingga).

Eksperimen

Proses pengukuran persis sama dengan yang dibahas di bagian 221. Gambar 222.1 adalah foto susunan kapasitor saat pengukuran

Hasil

Gambar 222.2 adalah kurva pengisian kapasitor dalam susunan seri. Dari bawah ke atas adalah kurva untuk satu kapasitor, dua kapasitor yang diseri, dan tiga kapasitor yang diseri. Tampak bahwa makin banyak kapasitor yang diseri maka makin cepat proses pengisian kapasitor.

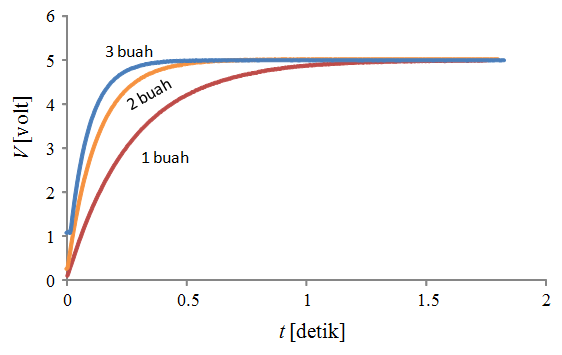
Gambar 222.3 adalah kurva pengisian kapasitor dalam susunan paralel. Dari atas ke bawah adalah kurva ntuk satu kapasitor, dua kapasitor yang diparalel, dan tiga kapasitor yang diparalel. Tampak bahwa makin banyak kapasitor yang diparalel maka makin lambat proses pengisian kapasitor.

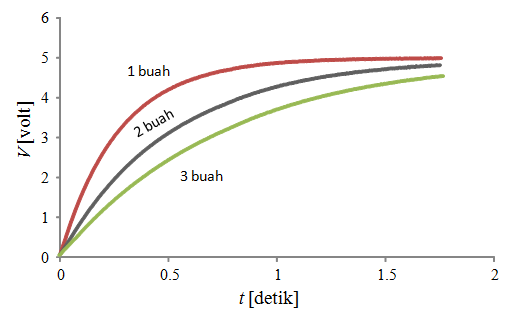
Perhitungan Kapasitansi

Untuk menghitung kapasitansi maka kita harus menggambar kurva \( \log(V_0 – V) \) terhadap waktu lalu mencari kemiringan kurva. Gambar 222.4 adalah kurva untuk kapasitor yang disusun secara seri dan Gambar 222.5 adalah kurva untuk kapasitor yang disusun secara paralel.

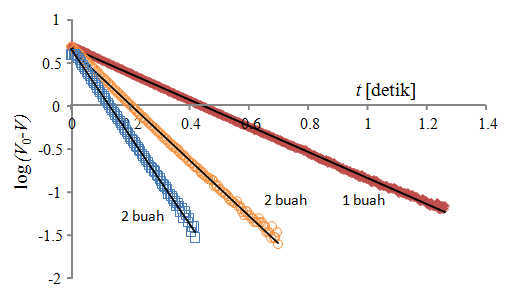
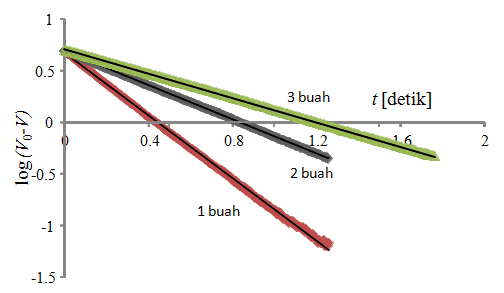
Dari gambar tersebut kita dapatkan gradien data seperti pada Tabel 222.1. Kemudian dari gradien kita hitung kapasitansi total menurut persamaan \( C = -0.693/(gradien \times R) \)

Tabel 222.1 Hasil perhitungan

Susunan kapasitor	Gradien	Kapasitansi total (mikrofarad)	Kapasitansi total/kapasitansi tunggal
Tunggal	-1,5127	8,18	1
Dua buah Seri	-3,2195	3,84	0,47 (kira-kira 1/2)
Tiga Buah Seri	-5,0532	2,45	0,3 (kira-kira 1/3)
Dua Buah Paralel	-0,8273	14,96	1,83 (kira-kira 2)
Tiga Buah Paralel	-0,5878	21,08	2,6 (kira-kira 3)

Tampak dari Tabel 222.1 bahwa:

1. Dua kapasitor sejenis yang disusun seri menghasilkan kapasitansi total setengah kapasitasi semula.
2. Tiga kapasitor sejenis yang disusun seri menghasilkan kapasitansi total sepertiga kapasitasi semula.
3. Dua kapasitor sejenis yang disusun paralel menghasilkan kapasitansi total dua kali kapasitasi semula
4. Tiga kapasitor sejenis yang disusun paralel menghasilkan kapasitansi total tiga kali kapasitasi semula

Hasil ini membuktikan persamaan rangkaian seri dan paralel kapasitor.