220: Fisika SMA: Pengisian dan Pengosongan Kapasitor

Sudah kita bahas bahwa kapasitor berfungsi untuk menyimpan muatan listrik. Ketika kapasitor dihubungkan dengan sumber tegangan maka muatan positif akan mengisi satu pelat kapasitor dan muatan negatif mengisi pelat yang satunya. Pengisian berlangsung terus hingga tercapai muatan maksimal yang memenuhi \( Q = C V \).

Karena muatan dari baterei harus mengalir ke arah pelat kapasitor maka dibutuhkan waktu untuk mengisi kapasitor. Pertanyaannya, berapa lama waktu tersebut?

Pengisian Kapasitor

Kalau kita menghubungkan langsung kapasitor ke sumber tegangan, maka waktu yang diperlukan untuk mengisi kapasitor hampir nol (lihat ilustrasi Gambar 220.1). Begitu saklar di-ON maka mauatan dari baterei langsung mengalir ke pelat kapasitor dan dalam waktu sekejap kapasitor penuh.

Tetapi, kalau cara ini yang dilakukan maka arus yang mengalir sangat besar dan bisa merusak kapasitor atau sumber tegangan. Terjadi lecutan arus yang sangat besar. Arus yang mengalir seperti impuls pada proses tumbukan. Jika waktu tumbukan sangat singkat maka gaya yang dihasilkan luar biasa besarnya.

Untuk mengamankan komponen maka arus yang mengalir tidak boleh terlalu besar. Untuk maksud tersebut maka dipasangan sebuah tahanan. Tahanan inilah yang memperkecil arus yang mengalit ke kapasitor. Rangkaian tampak pada Gambar 220.2. Akibat arus yang tidak besar maka diperlukan waktu yang lama untuk mengisi kapasitor. Tegangan antara dua kaki kapasitor akan naik dengan bertambahnya waktu. Ketika waktu sudah sangat lama maka tegangan antara dua kaki kapasitor persis sama dengan tegangan baterei.

Nilai kapasitansi dan nilai tahahan yang dipasang menentukan lama wakru pengisian kapasitor. Perubahan tegangan kapasitor sebagai fungsi waktu memenuhi persamaan

\( V = V_0 \left [ {1 – {\left ({1 \over 2} \right )}^{t/T} } \right ] \quad \quad \quad \quad \quad \quad (220.1) \)

di mana

\( V_0 \) adalah tegangan baterei atau sumber tegangan lain

\( t \) adalah waktu

\( T = 0,693 R C \)

\( R \) adalah nilai tahanan yang dipasang

\( C \) kapasitansi yang dipasang.

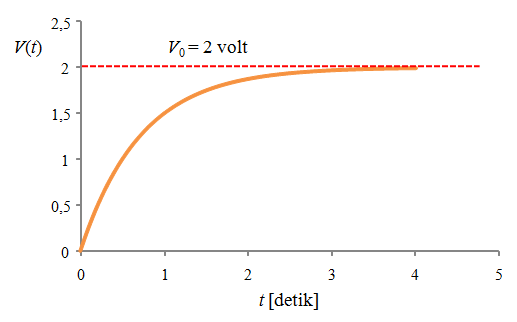
Bentuk kurva tegangan sebagai fungsi waktu akan tampak seperti pada Gambar 220.3. Kita lihat bahwa kurva mula-mula naik secara cepat. Lalu bertambah sangat lambat saat mendekati \( V_0 \).

Pengosongan Kapasitor

Kapasitor yang sudah berisi muatan dapat dikosongkan dengan menyambung langsung dua kaki. Tetapi cara ini mudah merusak kapasitor karena arur yang dihasilkan sangat tinggi. Cara aman adalah menghubungkan dua kaki kapasitor melalui sebuah hambatan. Hambatan berperan memperkecil arus sepertti pada Gambar 220.4. Arus yang mengalir kecil sehingga waktu yang diperlukan untuk mengosongkan kapasitor menjadi lama. Mengosongkan di sini artinya menggambungkan muatan positif dan negatif di dua pelat kapasitor sehingga masing-masing pelat menjadi netral.

Mula-mula tegangan kapasitor adalah \( V_0 \). Makain lama tegangan kapasitor makin kecil dan memenuhi persamaan

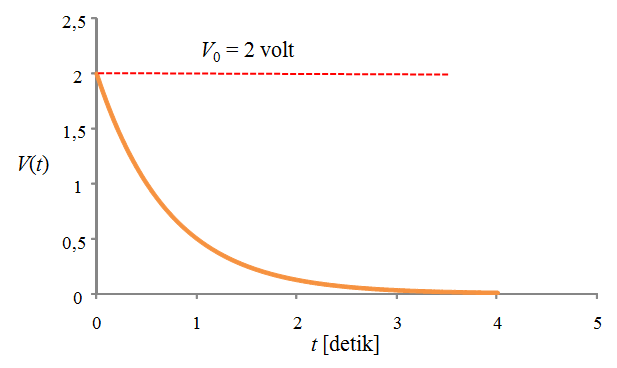
\( V = V_0 {\left ({1 \over 2} \right )}^{t/T} \quad \quad \quad \quad \quad \quad (220.2) \)

Bentuk kurva tegangan sebagai fungsi waktu seperti pada Gambar 220.5. Tampak bahwa kurva mula-mula turun secara cepat. Lalu berkurang sangat lambat saat mendekati nol volt.

Mengukur Kapasitansi

Kapasitansi adalah besaran yang sulit diukur. Multimeter tidak dapat digunakan untuk mengukur kapasitansi. Kapasitansi sering ditentukan dengan metode tidak langsung. Yang diukur adalah besaran lain. Dari besaran-besaran tersebut kita hitung kapasitansi.

Dari kurva pengisian dan pengosongan kapasitor maka kita dapat mengukur kapasitansi kapasitor. Bagaimana caranya?

Kita ambil logaritma persamaan (220.2) maka kita dapat menulis

\( \log V = \log V_0 +{t \over T} \log (1/2) \)

\( = \log V_0 -{t \over T} \log 2 \)

\( = \log V_0 -{\log 2 \over T} t \)

Persaman terakhir adalah persamaan linier \( y = a x + b \) dengan \( y = \log V \), \( a = – \log 2 /T \), dan \( b = \log V_0 \). Yang terpenting bagi kita adalah gradien kurva.

Untuk menentukan kapasitansi, kita tidak mengambar kurva \( V \) terhadap waktu, tetapi \( \log V \) terhadao waktu. Kurva yang diperoleh akan berupa garis lurus. Gradien garis lurus kita ukur. Gradien tersebut sama dengan \( – \log 2 /T \). Tetapi kita sudah dapatkan persamaan bahwa \( T = 0,693 R C \). Maka dengan mengukur \( R \) menggunakan multimeter, kita dapat menghitung \( C \).